For many years in the early days of computer-generated graphics, I was a designer of charts and graphs for business presentations. My book How to Lie with Charts coopted the title of the classic text on data misrepresentation, How to Lie with Statistics by Darrell Huff and Irving Geis.
I admit I have a high-school level familiarity with mathematics. My education sailed through trigonometry but ran aground short of calculus. I believe I do have a conceptual understanding of the differential and integral approaches to describing dynamics in equations and charts.
In my Charts book, I spend a chapter on the implied meaning of screen direction. It’s about the mental images we’ve formed as readers of Western languages (from left to right on the page implies the progress of time) and students of Mercator’s maps (up and down indicating North and South). It has always intrigued me that these paradigms influence so much of our routine perceptions and daily activities. I remark, for example, that movie directors seem to understand that a shot of an airplane flying from left to right somehow fairly portrays a journey from West to East, from Los Angeles to New York. No one needs to explain this bias to the audience, and film schools don’t need to train directors how to use it.
So I blame spatial stereotypes on Descartes and Mercator.
What bothers me, and the inspiration for this brief essay, is that, through the ages, our having to learn from the two-dimensional pages of books and drawings may have severely limited our understanding and interpretation of some essential elements of mathematics and therefore of physics.
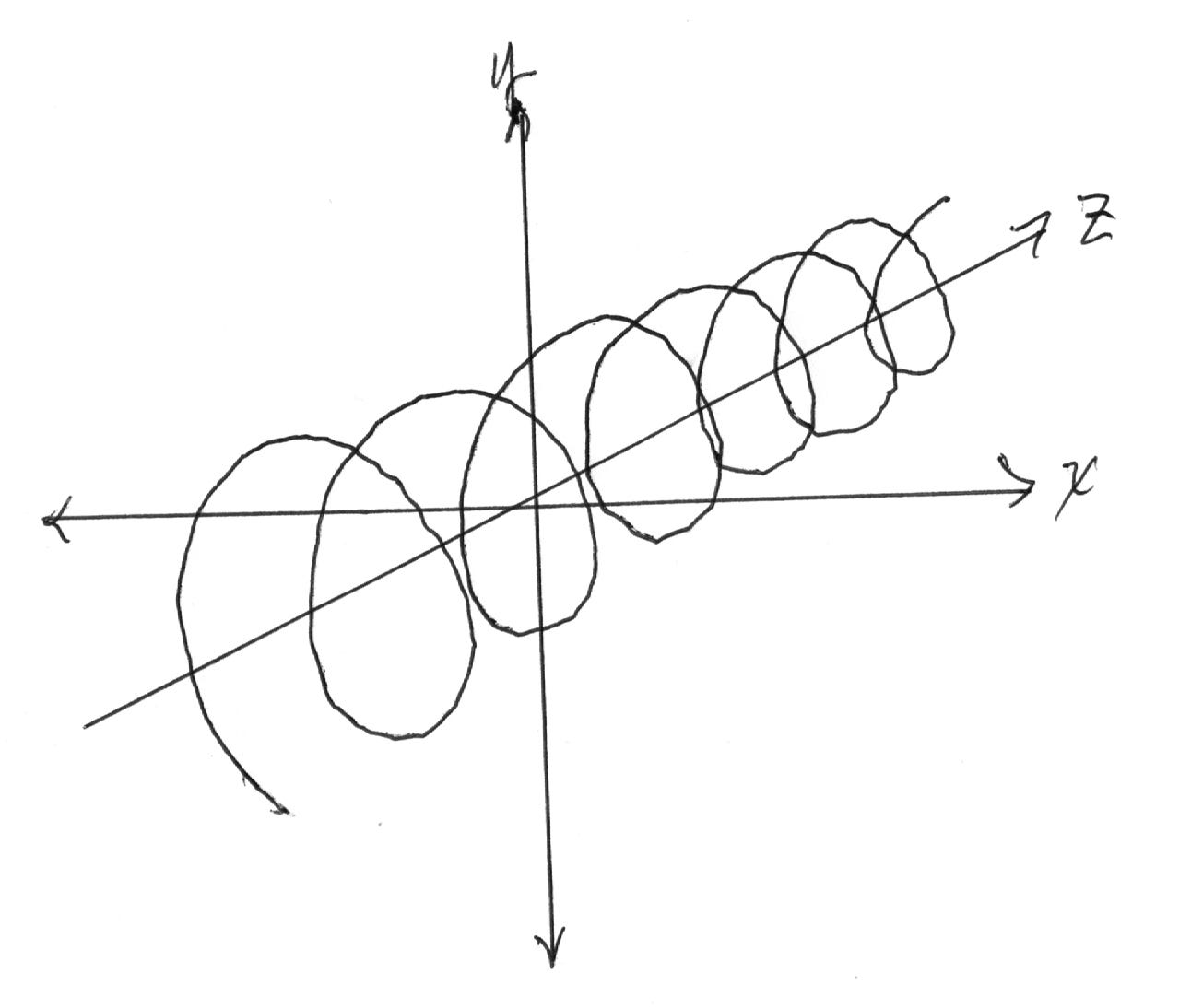
My favorite example of what I might call 2D bias is the basis of trigonometry, as exemplified by the sine wave. The math that describes a sine wave is, to me, bizarre and needlessly complex.
How might our understanding of wave functions be different if the likes of Descartes had visualized them—not on a drawing pad—but with the aid of a 3D (virtual reality) VR workspace?
A sine wave is a flattened spiral.
A spiral is defined by circular motion (an orbit) progressing through time.
The spiral’s diminishing orbit is the effect of entropy.
A spiral orbit that loses energy uniformly over time is a conic section (think about it!).
A spiral describes the pattern of water flowing down a drain or the swirling of stars around the central black hole of the Milky Way.
What about the famous two-slit problem in physics?
A beam of spiraling photons that is slightly off center of the target (as some even in a coherent transmission might be, if only minutely) can pass through both slits, one right after the other but seeming concurrent to the observer.
The photon beam is not a 2D wave but a 3D stream of particles propagated in a spiral.
Can matrix and wave mechanics of quantum theory thus be reconciled?
Please discuss among yourselves!
Stroke survivor Clifford Clovis obsessed over spirals, but he didn’t know why.
Feed your curiosity with a paid subscription to this Thinking About Thinking blog. With a paid subscription, you’ll gain access to all the content that’s here, including podcasts, and you’ll be helping us build our worldwide community through storytelling and self-expression.
If you’re a free subscriber here, upgrade to paid for $5 per month or $30 and get access to all content, including Thinking About Thinking book reviews, thoughtful essays, podcasts, and audiobooks.